Означення та формули
Таблиця формул скороченого множення
| Назва формули | Формула | Пояснення |
|---|---|---|
| Квадрат суми | (a + b)2 = a2 + 2ab + b2 | Квадрат суми двох чисел |
| Квадрат різниці | (a – b)2 = a2 – 2ab + b2 | Квадрат різниці двох чисел |
| Різниця квадратів | a2 – b2 = (a – b)(a + b) | Добуток суми та різниці двох чисел |
| Куб суми | (a + b)3 = a3 + 3a2b + 3ab2 + b3 | Куб суми двох чисел |
| Куб різниці | (a – b)3 = a3 – 3a2b + 3ab2 – b3 | Куб різниці двох чисел |
| Сума кубів | a3 + b3 = (a + b)(a2 – ab + b2) | Сума кубів двох чисел |
| Різниця кубів | a3 – b3 = (a – b)(a2 + ab + b2) | Різниця кубів двох чисел |
Таблиця відсотків і властивостей пропорції
| Операція | Формула | Опис |
|---|---|---|
| Знаходження відсотків від числа | \( P = \frac{p}{100} \cdot N \) | Щоб знайти відсотки від числа \( N \), множимо \( N \) на частку відсотків \( p \) у десятковому вигляді. |
| Знаходження числа за його відсотками | \( N = \frac{P}{p} \cdot 100 \) | Щоб знайти число \( N \) за відомим відсотком \( p \) і частиною \( P \). |
| Знаходження відсоткового відношення двох чисел | \( \text{Відсотки} = \frac{a}{b} \cdot 100 \) | Щоб знайти, скільки відсотків одне число становить від іншого. |
| Формула простих відсотків | \( A_n = A_0 \left(1 + \frac{p \cdot n}{100}\right) \) | Нарахування простих відсотків за кількість періодів \( n \). |
| Формула складних відсотків | \( A_n = A_0 \left(1 + \frac{p}{100}\right)^n \) | Нарахування складних відсотків за кількість періодів \( n \) |
| Пропорція | \( \frac{a}{b} = \frac{c}{d} \) | Пропорція виражає рівність двох відношень. Якщо \( \frac{a}{b} = \frac{c}{d} \), то \( a \cdot d = b \cdot c \). |
Таблиця степенів та їх властивостей
| Категорія | Формула | Опис |
|---|---|---|
| Степінь із натуральним показником | \( a^n \), де \( n \in \mathbb{N} \) | Число \( a \), піднесене до натурального степеня \( n \), є добутком \( n \) множників \( a \). |
| Степінь із цілим показником | \( a^{-n} = \frac{1}{a^n} \), де \( n \in \mathbb{Z} \) | Число \( a \), піднесене до від’ємного степеня \( n \), дорівнює частці \( 1 \), поділеній на \( a \) у степені \( n \). |
| Степінь із дробовим показником | \( a^{\frac{m}{n}} = \sqrt[n]{a^m} \), де \( m, n \in \mathbb{Z}, a > 0 \) | Степінь з дробовим показником визначає корінь \( n \)-го степеня із числа \( a \), піднесеного до степеня \( m \). |
| Множення степенів з однаковими основами | \( a^m \cdot a^n = a^{m+n} \) | При множенні степенів з однаковими основами показники додаються. |
| Ділення степенів з однаковими основами | \( \frac{a^m}{a^n} = a^{m-n} \) | При діленні степенів з однаковими основами показники віднімаються. |
| Степінь степеня | \( (a^m)^n = a^{m \cdot n} \) | При піднесенні степеня до степеня показники перемножуються. |
| Степінь добутку | \( (ab)^n = a^n \cdot b^n \) | Добуток чисел піднесених до одного й того самого степеня дорівнює добутку степенів. |
| Степінь частки | \( \left( \frac{a}{b} \right)^n = \frac{a^n}{b^n} \) | Частка чисел піднесених до одного й того самого степеня дорівнює частці степенів. |
Таблиця властивостей кореня \( n \)-го степеня
| Категорія | Формула | Опис |
|---|---|---|
| Корінь \( n \)-го степеня з числа | \( \sqrt[n]{a} = b \), де \( b^n = a \) | Корінь \( n \)-го степеня з числа \( a \) — це число \( b \), яке при піднесенні до степеня \( n \) дорівнює \( a \). |
| Множення коренів | \( \sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{ab} \) | Добуток коренів дорівнює кореню від добутку підкореневих виразів. |
| Ділення коренів | \( \frac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\frac{a}{b}} \) | Частка коренів дорівнює кореню від частки підкореневих виразів. |
| Корінь від кореня | \( \sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a} \) | Корінь від кореня можна об’єднати в один корінь з добутком показників коренів. |
| Степінь під коренем | \( \sqrt[n]{a^m} = a^{\frac{m}{n}} \) | Корінь \( n \)-го степеня від числа \( a^m \) дорівнює числу \( a \), піднесеному до степеня \( \frac{m}{n} \). |
| Степінь кореня | \( \left( \sqrt[n]{a} \right)^m = \sqrt[n]{a^m} \) | Корінь \( n \)-го степеня числа, піднесеного до степеня \( m \), дорівнює кореню від числа \( a^m \). |
| Корінь добутку | \( \sqrt[n]{ab} = \sqrt[n]{a} \cdot \sqrt[n]{b} \) | Корінь від добутку двох чисел дорівнює добутку коренів від кожного числа окремо. |
| Корінь квадрата числа | \( \sqrt{a^2} = |a| \) | Корінь квадратний із числа \( a^2 \) дорівнює модулю числа \( a \). |
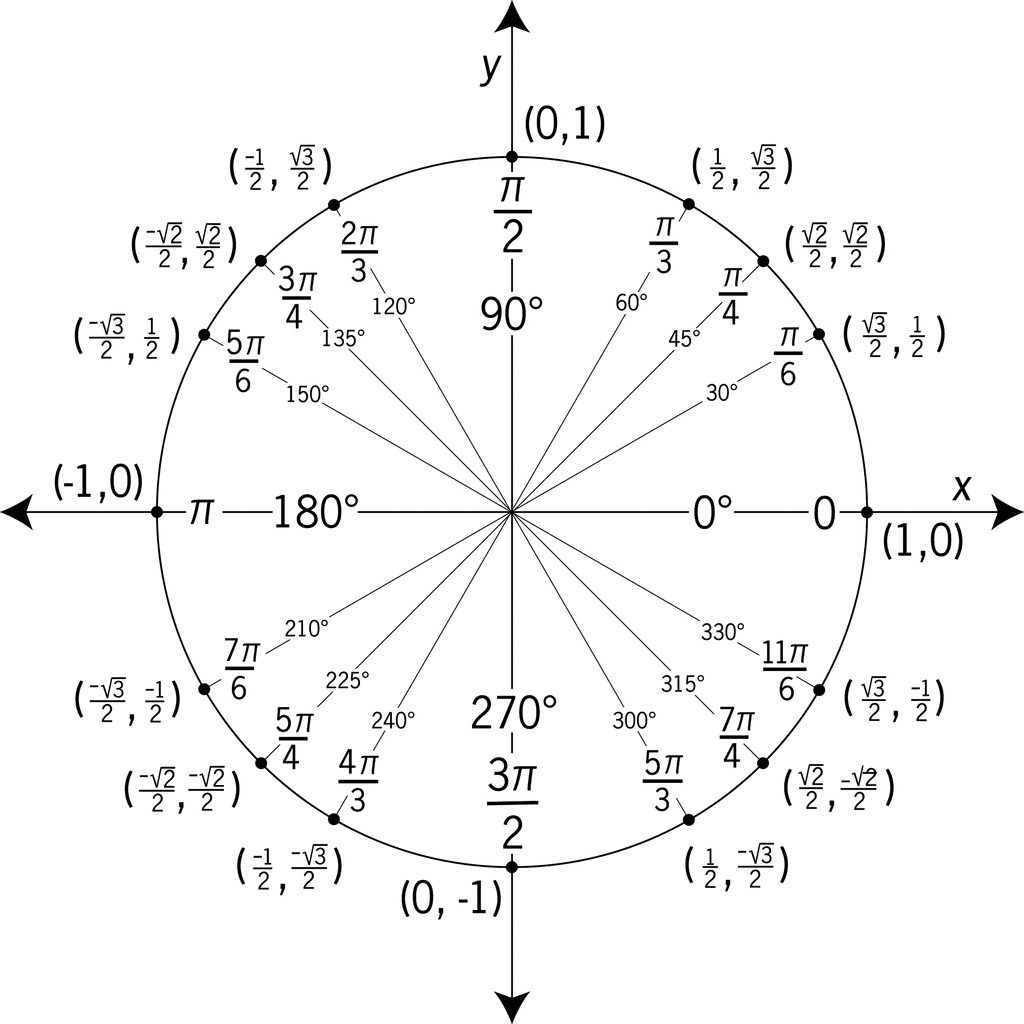
Таблиця радіанної міри кутів
| Градуси | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Радіани | 0 | \( \frac{\pi}{6} \) | \( \frac{\pi}{4} \) | \( \frac{\pi}{3} \) | \( \frac{\pi}{2} \) | \( \frac{2\pi}{3} \) | \( \frac{3\pi}{4} \) | \( \frac{5\pi}{6} \) | \( \pi \) | \( \frac{7\pi}{6} \) | \( \frac{5\pi}{4} \) | \( \frac{4\pi}{3} \) | \( \frac{3\pi}{2} \) | \( \frac{5\pi}{3} \) | \( \frac{7\pi}{4} \) | \( \frac{11\pi}{6} \) | \( 2\pi \) |
Формули коренів найпростіших тригонометричних рівнянь
| Тип рівняння | Формула | Корені |
|---|---|---|
| \( \sin x = a \) | \( \sin x = a \) | \( x = (-1)^n \arcsin(a) + n\pi \), де \( n \in \mathbb{Z} \), \( |a| \leq 1 \) |
| \( \cos x = a \) | \( \cos x = a \) | \( x = \pm \arccos(a) + 2n\pi \), де \( n \in \mathbb{Z} \), \( |a| \leq 1 \) |
| \( tg x = a \) | \( tg x = a \) | \( x = arctg(a) + n\pi \), де \( n \in \mathbb{Z} \), \( a \in \mathbb{R} \) |
| \( ctg x = a \) | \( ctg x = a \) | \( x = \text{arcctg}(a) + n\pi \), де \( n \in \mathbb{Z} \), \( a \in \mathbb{R} \) |
Тригонометричні рівняння для значень 0, 1, -1
| Тип рівняння | Загальна форма | Розв’язок |
|---|---|---|
| \( \sin x = 0 \) | \( \sin x = 0 \) | \( x = n\pi \), де \( n \in \mathbb{Z} \). |
| \( \sin x = 1 \) | \( \sin x = 1 \) | \( x = \frac{\pi}{2} + 2n\pi \), де \( n \in \mathbb{Z} \). |
| \( \sin x = -1 \) | \( \sin x = -1 \) | \( x = \frac{3\pi}{2} + 2n\pi \), де \( n \in \mathbb{Z} \). |
| \( \cos x = 0 \) | \( \cos x = 0 \) | \( x = \frac{\pi}{2} + n\pi \), де \( n \in \mathbb{Z} \). |
| \( \cos x = 1 \) | \( \cos x = 1 \) | \( x = 2n\pi \), де \( n \in \mathbb{Z} \). |
| \( \cos x = -1 \) | \( \cos x = -1 \) | \( x = \pi + 2n\pi \), де \( n \in \mathbb{Z} \). |
| \( tg x = 0 \) | \( tg x = 0 \) | \( x = n\pi \), де \( n \in \mathbb{Z} \). |
| \( tg x = 1 \) | \( tg x = 1 \) | \( x = \frac{\pi}{4} + n\pi \), де \( n \in \mathbb{Z} \). |
| \( tg x = -1 \) | \( tg x = -1 \) | \( x = \frac{3\pi}{4} + n\pi \), де \( n \in \mathbb{Z} \). |
| \( ctg x = 0 \) | \( ctg x = 0 \) | \( x = \frac{\pi}{2} + n\pi \), де \( n \in \mathbb{Z} \). |
| \( ctg x = 1 \) | \( ctg x = 1 \) | \( x = \frac{\pi}{4} + n\pi \), де \( n \in \mathbb{Z} \). |
| \( ctg x = -1 \) | \( ctg x = -1 \) | \( x = \frac{3\pi}{4} + n\pi \), де \( n \in \mathbb{Z} \). |
Тригонометричні формули
| Тип формули | Формули |
|---|---|
| Формули для зведення аргументу | \( \sin(-x) = -\sin(x) \) \( \cos(-x) = \cos(x) \) \( tg(-x) = -tg(x) \) \( ctg(-x) = -ctg(x) \) |
| Формули суми та різниці кутів | Для суми: Для різниці: |
| Формули суми та різниці функцій | Для суми: \( \sin(\alpha) + \sin(\beta) = 2 \sin\left(\frac{\alpha + \beta}{2}\right) \cos\left(\frac{\alpha – \beta}{2}\right) \) \( \cos(\alpha) + \cos(\beta) = 2 \cos\left(\frac{\alpha + \beta}{2}\right) \cos\left(\frac{\alpha – \beta}{2}\right) \) Для різниці: \( \sin(\alpha) – \sin(\beta) = 2 \cos\left(\frac{\alpha + \beta}{2}\right) \sin\left(\frac{\alpha – \beta}{2}\right) \) \( \cos(\alpha) – \cos(\beta) = -2 \sin\left(\frac{\alpha + \beta}{2}\right) \sin\left(\frac{\alpha – \beta}{2}\right) \) |
| Формули подвійного кута | \( \sin(2x) = 2 \sin(x) \cos(x) \) \( \cos(2x) = \cos^2(x) – \sin^2(x) = 2 \cos^2(x) – 1 = 1 – 2 \sin^2(x) \) \( tg(2x) = \frac{2 tg(x)}{1 – tg^2(x)} \) \( ctg(2x) = \frac{ctg^2(x) – 1}{2 ctg(x)} \) |
| Формули половинного кута | \( \sin\left(\frac{x}{2}\right) = \pm\sqrt{\frac{1 – \cos(x)}{2}} \) \( \cos\left(\frac{x}{2}\right) = \pm\sqrt{\frac{1 + \cos(x)}{2}} \) \( tg\left(\frac{x}{2}\right) = \frac{1 – \cos(x)}{\sin(x)} = \frac{\sin(x)}{1 + \cos(x)} \) |
| Тотожності для добутків | \( \sin(\alpha) \sin(\beta) = \frac{1}{2} [\cos(\alpha – \beta) – \cos(\alpha + \beta)] \) \( \cos(\alpha) \cos(\beta) = \frac{1}{2} [\cos(\alpha – \beta) + \cos(\alpha + \beta)] \) \( \sin(\alpha) \cos(\beta) = \frac{1}{2} [\sin(\alpha + \beta) + \sin(\alpha – \beta)] \) |
| Тип прогресії | Формула \(n\)-го члена | Сума перших \(n\) членів |
|---|---|---|
| Арифметична прогресія | \(a_n = a_1 + (n – 1) \cdot d\) | \(S_n = \frac{n}{2} \cdot (a_1 + a_n)\) або \(S_n = \frac{n}{2} \cdot (2a_1 + (n – 1) \cdot d)\) |
| Геометрична прогресія | \(a_n = a_1 \cdot q^{n – 1}\) | \(S_n = a_1 \cdot \frac{1 – q^n}{1 – q}, \quad q \neq 1\) Сума нескінченної прогресії (якщо \( |q| < 1 \)): \( S = \frac{a_1}{1 – q} \) |
Логарифм та його властивості
| Формула | Пояснення |
|---|---|
| \( \log_a 1 = 0 \) | Логарифм одиниці при будь-якій основі дорівнює 0, оскільки \( a^0 = 1 \). |
| \( \log_a a = 1 \) | Логарифм числа при тій самій основі дорівнює 1, оскільки \( a^1 = a \). |
| \( \log_a (x \cdot y) = \log_a x + \log_a y \) | Логарифм добутку двох чисел дорівнює сумі логарифмів цих чисел. |
| \( \log_a \left(\frac{x}{y}\right) = \log_a x – \log_a y \) | Логарифм частки двох чисел дорівнює різниці логарифмів. |
| \( \log_a (x^n) = n \cdot \log_a x \) | Логарифм степеня числа дорівнює добутку показника степеня на логарифм основи. |
| \( \log_a \sqrt[n]{x} = \frac{1}{n} \log_a x \) | Логарифм кореня дорівнює логарифму підкореневого виразу, поділеному на степінь кореня. |
| \( \log_a b = \frac{\log_c b}{\log_c a} \) | Формула зміни основи логарифма: для обчислення логарифма з новою основою можна використати логарифми з довільною основою. |
| \( \log_a (1/x) = -\log_a x \) | Логарифм оберненого числа дорівнює протилежному значенню логарифма числа. |
| \( \log_a b = \frac{1}{\log_b a} \) | Наслідок 1: формула для зміни основи логарифма через обернену функцію. |
| \( \log_a b = \log_{a^k} b^k \) | Наслідок 2: логарифм числа \( b \) з основою \( a \), при цьому обидві величини підносяться до степеня \( k \). |
Таблиця похідних деяких функцій
| Функція \( f \) | Похідна \( f’ \) | Функція \( f \) | Похідна \( f’ \) |
|---|---|---|---|
| \( k \, (\text{стала}) \) | 0 | \( x \) | 1 |
| \( x^\alpha \) | \( \alpha x^{\alpha-1} \) | \( \sqrt{x} \) | \( \frac{1}{2\sqrt{x}} \) |
| \( \sin x \) | \( \cos x \) | \( \cos x \) | \( -\sin x \) |
| \( tg x \) | \( \frac{1}{\cos^2 x} \) | \( ctg x \) | \( -\frac{1}{\sin^2 x} \) |
| \( \arcsin x \) | \( \frac{1}{\sqrt{1 – x^2}} \) | \( \arccos x \) | \( -\frac{1}{\sqrt{1 – x^2}} \) |
| \( arctg x \) | \( \frac{1}{1 + x^2} \) | \( arcctg x \) | \( -\frac{1}{1 + x^2} \) |
Правила диференціювання
\( (f + g)’ = f’ + g’ \)
\( (f \cdot g)’ = f’ \cdot g + f \cdot g’ \)
\( \left( \frac{f}{g} \right)’ = \frac{f’ \cdot g – f \cdot g’}{g^2} \)
Рівняння дотичної
\( y = f'(x_0)(x – x_0) + f(x_0) \)
Таблиця первісних (невизначених інтегралів)
| Функція \( f(x) \) | Загальний вигляд первісних \( F(x) + C \), де \( C \) — довільна стала | Запис за допомогою невизначеного інтегралу |
|---|---|---|
| 0 | \( C \) | \( \int 0 \, dx = C \) |
| 1 | \( x + C \) | \( \int 1 \, dx = x + C \) |
| \( k \, (\text{стала}) \) | \( kx + C \) | \( \int k \, dx = kx + C \) |
| \( x^\alpha \, (\alpha \neq -1) \) | \( \frac{x^{\alpha + 1}}{\alpha + 1} + C \) | \( \int x^\alpha \, dx = \frac{x^{\alpha + 1}}{\alpha + 1} + C \, (\alpha \neq -1) \) |
| \( \frac{1}{x} \) | \( \ln |x| + C \) | \( \int \frac{1}{x} \, dx = \ln |x| + C \) |
| \( \sin x \) | \( -\cos x + C \) | \( \int \sin x \, dx = -\cos x + C \) |
| \( \cos x \) | \( \sin x + C \) | \( \int \cos x \, dx = \sin x + C \) |
| \( \frac{1}{\cos^2 x} \) | \( tg x + C \) | \( \int \frac{dx}{\cos^2 x} = tg x + C \) |
| \( \frac{1}{\sin^2 x} \) | \( -ctg x + C \) | \( \int \frac{dx}{\sin^2 x} = -ctg x + C \) |
| \( e^x \) | \( e^x + C \) | \( \int e^x \, dx = e^x + C \) |
| \( a^x \, (a > 0, a \neq 1) \) | \( \frac{a^x}{\ln a} + C \) | \( \int a^x \, dx = \frac{a^x}{\ln a} + C \) |
Основні правила інтегрування
\( \int f(x) \, dx = F(x) + C \)
\( \int k \cdot f(x) \, dx = k \cdot \int f(x) \, dx \)
\( \int (f(x) + g(x)) \, dx = \int f(x) \, dx + \int g(x) \, dx \)
\( \int (f(x) – g(x)) \, dx = \int f(x) \, dx – \int g(x) \, dx \)
\( \int f(g(x)) \cdot g'(x) \, dx = \int f(u) \, du \), де \( u = g(x) \)
Основні елементи комбінаторики
План правильного вибору формул
Щоб правильно вибрати формулу для розв’язання комбінаторної задачі, виконайте такі кроки:
- З’ясуйте, чи є повторення: Чи дозволяється повторення елементів у розміщеннях, перестановках або комбінаціях?
- Визначте тип задачі: Вам потрібно знайти кількість варіантів розміщення, перестановки або комбінації?
- З’ясуйте порядок елементів: Чи важливий порядок елементів у варіантах?
- Виберіть правило комбінаторики:
- – Правило суми: Якщо подія може відбутися одним із кількох способів, то кількість способів дорівнює сумі кількостей кожного з цих способів.
- – Правило добутку: Якщо подія складається з кількох незалежних етапів, то кількість способів її здійснення дорівнює добутку кількостей способів кожного з етапів.
- Виберіть формулу: Відповідно до відповіді на попередні запитання виберіть одну з формул:
- – Якщо порядок елементів важливий і повторення не дозволяється — використовуйте розміщення без повторень.
- – Якщо порядок елементів важливий і повторення дозволяється — використовуйте розміщення з повтореннями.
- – Якщо порядок елементів не важливий і повторення не дозволяється — використовуйте комбінації без повторень.
- – Якщо порядок елементів не важливий і повторення дозволяється — використовуйте комбінації з повтореннями.
- – Якщо потрібно знайти кількість перестановок — використовуйте перестановки.
1. Факторіал числа
Формула для факторіала:
\[
n! = 1 \cdot 2 \cdot 3 \cdot \dots \cdot n
\]
Приклад: \(5! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 = 120\)
2. Розміщення
2.1 Розміщення без повторень
Формула для розміщення без повторень:
\[
A_n^k = \frac{n!}{(n – k)!}
\]
Приклад: Скільки можна скласти двоцифрових чисел з цифр \(1, 2, 3, 4\)?
\[
A_4^2 = \frac{4!}{(4 – 2)!} = 12
\]
2.2 Розміщення з повтореннями
Формула для розміщення з повтореннями:
\[
A_n^k = n^k
\]
Приклад: Скільки можна скласти двоцифрових чисел з цифр \(1, 2, 3\), якщо цифри можуть повторюватися?
\[
A_3^2 = 3^2 = 9
\]
3. Перестановки
3.1 Перестановки без повторень
Формула для перестановок без повторень:
\[
P_n = n!
\]
Приклад: Скільки існує способів упорядкувати 4 цифри \(1, 2, 3, 4\)?
\[
P_4 = 4! = 24
\]
3.2 Перестановки з повтореннями
Формула для перестановок з повтореннями:
\[
P = \frac{n!}{n_1! \cdot n_2! \cdot \dots \cdot n_k!}
\]
Приклад: Скількома різними способами можна упорядкувати слово “LEVEL”, де \(E\) повторюється двічі?
\[
P = \frac{5!}{2!} = 60
\]
4. Комбінації
4.1 Комбінації без повторень
Формула для комбінацій без повторень:
\[
C_n^k = \frac{n!}{k!(n – k)!}
\]
Приклад: Скільки існує способів вибрати 2 кульки з набору з 4-х кульок?
\[
C_4^2 = \frac{4!}{2!(4 – 2)!} = 6
\]
4.2 Комбінації з повтореннями
Формула для комбінацій з повтореннями:
\[
C_n^k = \frac{(n+k-1)!}{k!(n-1)!}
\]
Приклад: Скількома способами можна вибрати 2 кульки з 3 кольорів, якщо кульки можуть повторюватися?
\[
C_3^2 = \frac{(3+2-1)!}{2!(3-1)!} = 6
\]
5. Біном Ньютона
Формула для розкладу бінома:
\[
(a + b)^n = \sum_{k=0}^{n} C_n^k \cdot a^{n-k} \cdot b^k
\]
Приклад: Розкласти \( (x + y)^3 \):
\[
(x + y)^3 = C_3^0 x^3 + C_3^1 x^2y + C_3^2 xy^2 + C_3^3 y^3 = x^3 + 3x^2y + 3xy^2 + y^3
\]
Теорія ймовірностей та статистика
1. Основні поняття ймовірностей
Ймовірність події — це числове значення, яке виражає шанс або можливість настання певної події.
Формула класичної ймовірності:
\[
P(A) = \frac{m}{n}
\]
де:
- \(m\) — кількість сприятливих для події \(A\) результатів;
- \(n\) — загальна кількість можливих результатів.
Приклад: Якщо монету підкидають один раз, ймовірність випаду “орла” дорівнює:
\[
P(A) = \frac{1}{2}
\]
2. Основні формули ймовірностей
2.1 Закон суми ймовірностей
Ймовірність того, що настане хоча б одна з двох взаємовиключних подій:
\[
P(A \cup B) = P(A) + P(B)
\]
2.2 Закон добутку ймовірностей
Ймовірність того, що одночасно настануть дві незалежні події:
\[
P(A \cap B) = P(A) \cdot P(B)
\]
2.3 Умовна ймовірність
Ймовірність настання події \(A\) за умови, що подія \(B\) вже відбулася:
\[
P(A | B) = \frac{P(A \cap B)}{P(B)}
\]
2.4 Формула повної ймовірності
Якщо подія \(B\) може відбутися тільки разом з однією з подій \(A_1, A_2, \dots, A_n\), то:
\[
P(B) = P(A_1)P(B | A_1) + P(A_2)P(B | A_2) + \dots + P(A_n)P(B | A_n)
\]
2.5 Формула Байєса
Формула для обчислення умовної ймовірності події:
\[
P(A_i | B) = \frac{P(A_i)P(B | A_i)}{P(B)}
\]
3. Середні величини
Середня величина (математичне сподівання) випадкової величини \(X\) обчислюється за формулою:
\[
E(X) = \sum_{i} x_i \cdot P(x_i)
\]
де \(x_i\) — можливі значення величини, а \(P(x_i)\) — ймовірності цих значень.
4. Дисперсія та середньоквадратичне відхилення
Дисперсія випадкової величини \(X\) обчислюється за формулою:
\[
D(X) = E(X^2) – [E(X)]^2
\]
Середньоквадратичне відхилення:
\[
\sigma(X) = \sqrt{D(X)}
\]
5. Основні статистичні величини
| Назва | Позначення | Формула |
|---|---|---|
| Вибіркове середнє | \(\bar{x}\) | \(\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i\) |
| Медіана | \(Me\) | Значення, яке ділить вибірку на дві рівні частини |
| Мода | \(Mo\) | Значення, яке найчастіше зустрічається у вибірці |
| Дисперсія | \(D\) | \(D = \frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})^2\) |
| Середньоквадратичне відхилення | \(\sigma\) | \(\sigma = \sqrt{D}\) |
6. Правило суми та добутку ймовірностей
- Правило суми: Якщо події взаємовиключні, то ймовірність того, що відбудеться одна з них, дорівнює сумі їх ймовірностей: \(P(A \cup B) = P(A) + P(B)\).
- Правило добутку: Якщо події незалежні, то ймовірність їх одночасного настання дорівнює добутку їх ймовірностей: \(P(A \cap B) = P(A) \cdot P(B)\).
Вибіркове середнє та Дисперсія
1. Вибіркове середнє
Вибіркове середнє — це середнє арифметичне всіх значень вибірки. Воно використовується для того, щоб визначити “середнє” значення даних у наборі спостережень. Якщо у вас є \( n \) значень \( x_1, x_2, …, x_n \), вибіркове середнє обчислюється за формулою:
\[
\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i
\]
- \( \bar{x} \) — вибіркове середнє (середнє арифметичне)
- \( x_i \) — кожне окреме значення з вибірки
- \( n \) — загальна кількість значень у вибірці
Приклад:
Нехай у вас є вибірка значень: \( 3, 7, 8, 5, 10 \). Для того щоб знайти вибіркове середнє:
\[
\text{Сума значень} = 3 + 7 + 8 + 5 + 10 = 33
\]
\[
\bar{x} = \frac{33}{5} = 6.6
\]
Отже, вибіркове середнє \( \bar{x} = 6.6 \).
2. Дисперсія
Дисперсія показує, наскільки сильно значення даних розсіюються від вибіркового середнього. Вона використовується для оцінки варіативності даних і розраховується за формулою:
\[
D = \frac{1}{n} \sum_{i=1}^{n} (x_i – \bar{x})^2
\]
- \( D \) — дисперсія
- \( x_i \) — кожне значення вибірки
- \( \bar{x} \) — вибіркове середнє
- \( n \) — кількість значень у вибірці
Приклад:
Нехай у вас є вибірка значень: \( 3, 7, 8, 5, 10 \), і вибіркове середнє \( \bar{x} = 6.6 \).
Розрахуємо дисперсію:
\[
(3 – 6.6)^2 = 12.96,\quad (7 – 6.6)^2 = 0.16,\quad (8 – 6.6)^2 = 1.96
\]
\[
(5 – 6.6)^2 = 2.56,\quad (10 – 6.6)^2 = 11.56
\]
Сума квадратичних відхилень:
\[
12.96 + 0.16 + 1.96 + 2.56 + 11.56 = 29.2
\]
Розраховуємо дисперсію:
\[
D = \frac{29.2}{5} = 5.84
\]
Отже, дисперсія \( D = 5.84 \).