Функції та їх графіки

Головна » Алгебра – формули та означення » Функції та їх графіки

Графік функції \( y = \sin x \)

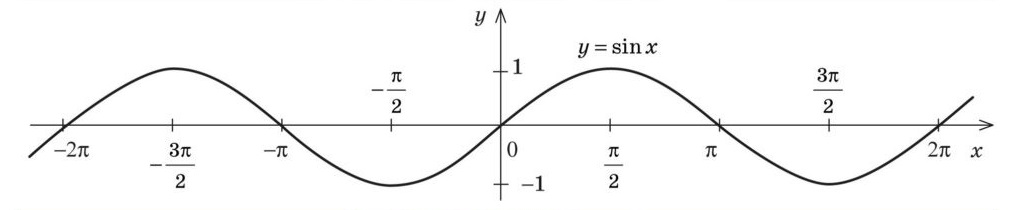
Властивості функції \( y = \sin x \)

ВластивістьОпис
Область визначення\( D(y) = \mathbb{R} \), тобто функція визначена на всій множині дійсних чисел.
Область значень\( E(y) = [-1; 1] \), функція набуває значень від \(-1\) до \(1\).
ПеріодичністьФункція є періодичною з періодом \( 2\pi \), тобто \( \sin(x + 2\pi) = \sin x \).
ПарністьФункція є непарною: \( \sin(-x) = -\sin(x) \).
Зростання і спаданняНа інтервалі \( \left[-\frac{\pi}{2}; \frac{\pi}{2}\right] \) функція зростає, на інтервалі \( \left[\frac{\pi}{2}; \frac{3\pi}{2}\right] \) — спадає.
Нулі функції\( x = n\pi \), де \( n \in \mathbb{Z} \) (кратні числа пі).
Максимуми і мінімумиМаксимуми: \( x = \frac{\pi}{2} + 2n\pi \), мінімуми: \( x = \frac{3\pi}{2} + 2n\pi \), де \( n \in \mathbb{Z} \).

 

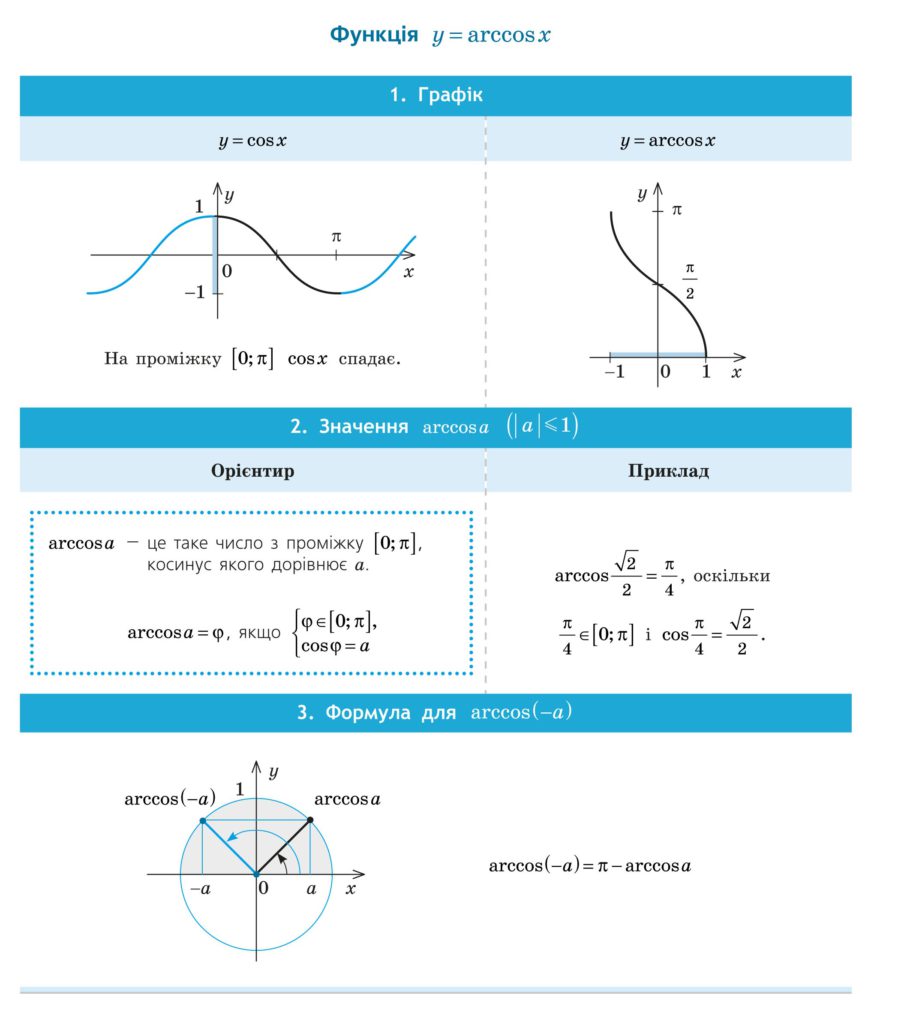
Графік функції \( y = \cos x \)

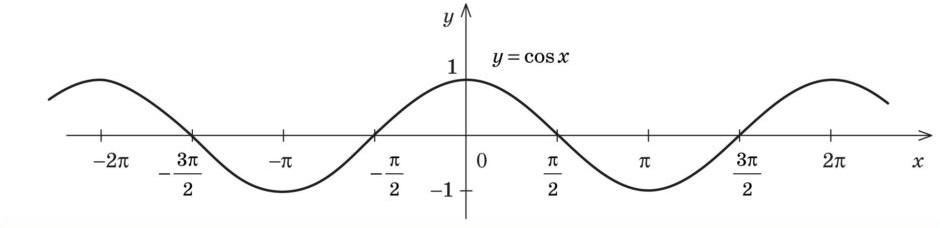
Властивості функції \( y = \cos x \)

ВластивістьОпис
Область визначення\( D(y) = \mathbb{R} \), тобто функція визначена на всій множині дійсних чисел.
Область значень\( E(y) = [-1; 1] \), функція набуває значень від \(-1\) до \(1\).
ПеріодичністьФункція є періодичною з періодом \( 2\pi \), тобто \( \cos(x + 2\pi) = \cos x \).
ПарністьФункція є парною: \( \cos(-x) = \cos(x) \).
Зростання і спаданняНа інтервалі \( \left[0; \pi\right] \) функція спадає, на інтервалі \( \left[\pi; 2\pi\right] \) — зростає.
Нулі функції\( x = \frac{\pi}{2} + n\pi \), де \( n \in \mathbb{Z} \).
Максимуми і мінімумиМаксимуми: \( x = 2n\pi \), мінімуми: \( x = \pi + 2n\pi \), де \( n \in \mathbb{Z} \).

 

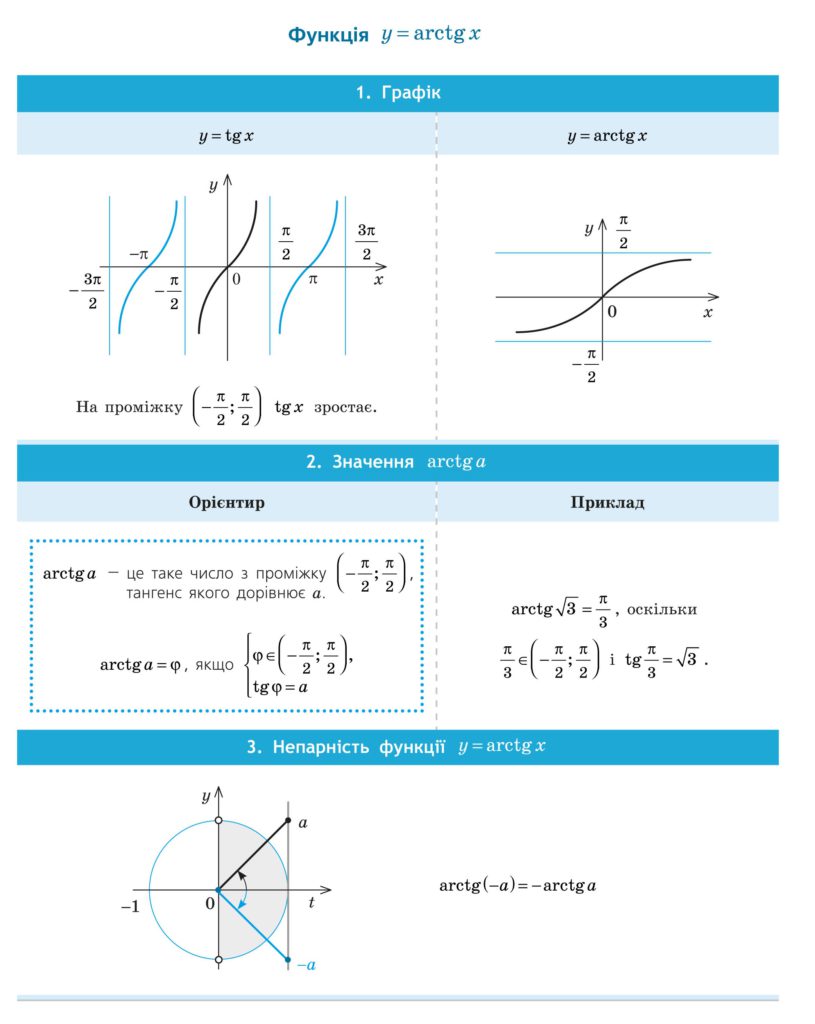
Властивості функції \( y = tg x \)

ВластивістьОпис
Область визначення\( D(y) = \mathbb{R} \setminus \left( \frac{\pi}{2} + n\pi \right), n \in \mathbb{Z} \), функція не визначена в точках \( x = \frac{\pi}{2} + n\pi \).
Область значень\( E(y) = \mathbb{R} \), функція набуває всіх дійсних значень.
ПеріодичністьФункція є періодичною з періодом \( \pi \), тобто \( tg(x + \pi) = tg x \).
ПарністьФункція є непарною: \( tg(-x) = -tg(x) \).
ЗростанняФункція є зростаючою на кожному інтервалі \( \left( -\frac{\pi}{2} + n\pi; \frac{\pi}{2} + n\pi \right), n \in \mathbb{Z} \).
Нулі функції\( x = n\pi \), де \( n \in \mathbb{Z} \).
АсимптотиФункція має вертикальні асимптоти при \( x = \frac{\pi}{2} + n\pi \), де \( n \in \mathbb{Z} \).

Графік функції \( y = tg x \)

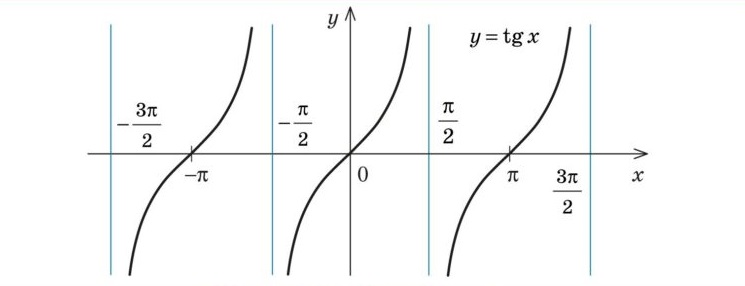
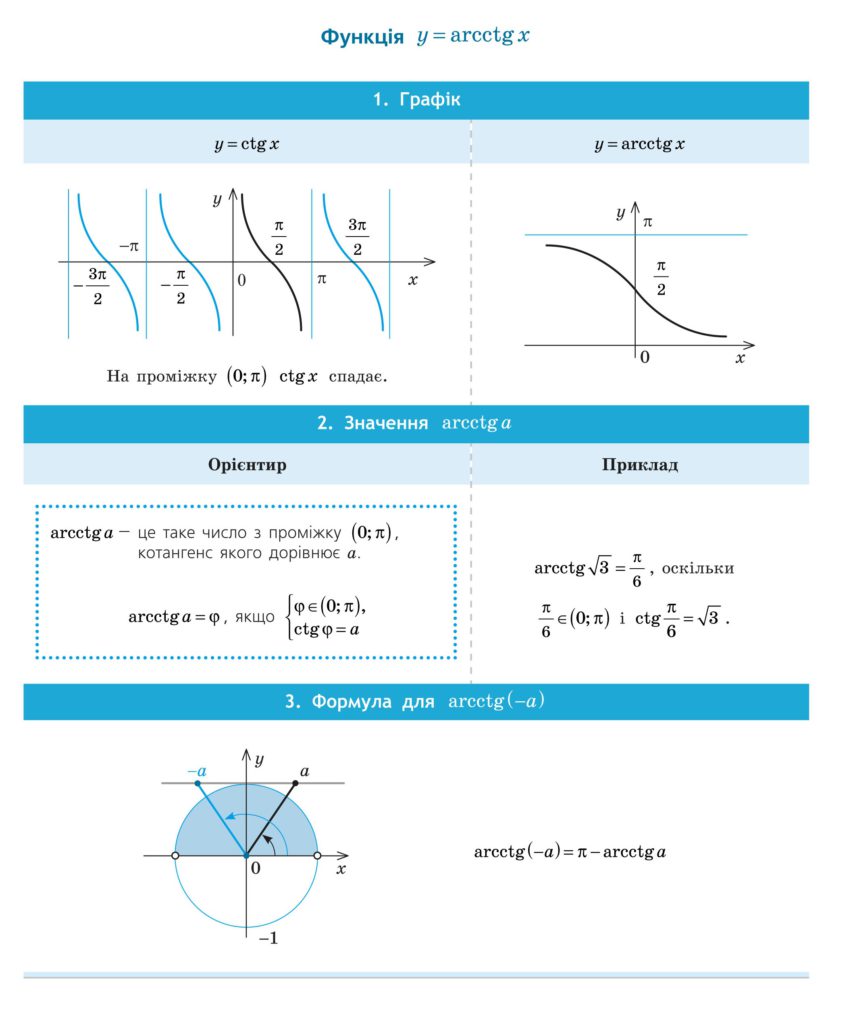
Властивості функції \( y = ctg x \)

Властивість Опис
Область визначення \( D(y) = \mathbb{R} \setminus \left( n\pi \right), n \in \mathbb{Z} \), функція не визначена в точках \( x = n\pi \).
Область значень \( E(y) = \mathbb{R} \), функція набуває всіх дійсних значень.
Періодичність Функція є періодичною з періодом \( \pi \), тобто \( \cot(x + \pi) = \cot x \).
Парність Функція є непарною: \( ctg(-x) = -ctg(x) \).
Зростання Функція є спадною на кожному інтервалі \( \left( 0 + n\pi; \pi + n\pi \right), n \in \mathbb{Z} \).
Нулі функції \( x = \frac{\pi}{2} + n\pi \), де \( n \in \mathbb{Z} \).
Асимптоти Функція має вертикальні асимптоти при \( x = n\pi \), де \( n \in \mathbb{Z} \).

Графік функції \( y = ctg x \)

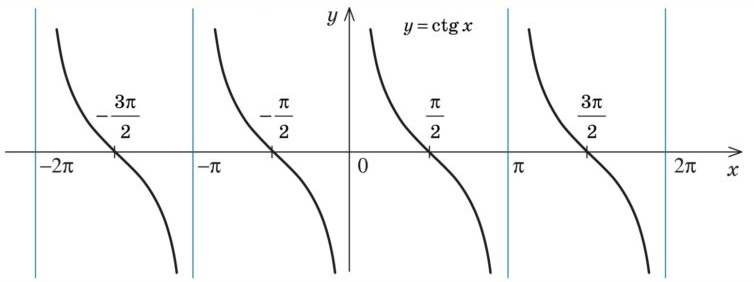
Властивості показникової функції

Властивості показникової функції

№ Властивість Опис
1 Область визначення Функція \( y = a^x \) визначена на всій множині дійсних чисел \( \mathbb{R} \), тобто \( D(y) = \mathbb{R} \).
2 Область значень Значення функції завжди додатні: \( y > 0 \), тому область значень — \( (0; +\infty) \).
3 Зростання або спадання
  • Якщо \( a > 1 \), то функція \( y = a^x \) є зростаючою.
  • Якщо \( 0 < a < 1 \), то функція \( y = a^x \) є спадною.
4 Поведінка при \( x \to +\infty \) та \( x \to -\infty \)
  • Якщо \( a > 1 \), при \( x \to +\infty \) функція необмежено зростає, при \( x \to -\infty \) прагне до нуля.
  • Якщо \( 0 < a < 1 \), при \( x \to +\infty \) функція прямує до нуля, при \( x \to -\infty \) необмежено зростає.
5 Перетин з віссю ординат Графік перетинає вісь ординат у точці \( (0, 1) \), тобто \( y(0) = 1 \) для будь-якого \( a > 0 \).
6 Неперервність і диференційованість Функція є неперервною та диференційованою на всій області визначення.
7 Асимптота Горизонтальна асимптота графіка: \( y = 0 \), але графік не перетинає вісь абсцис.
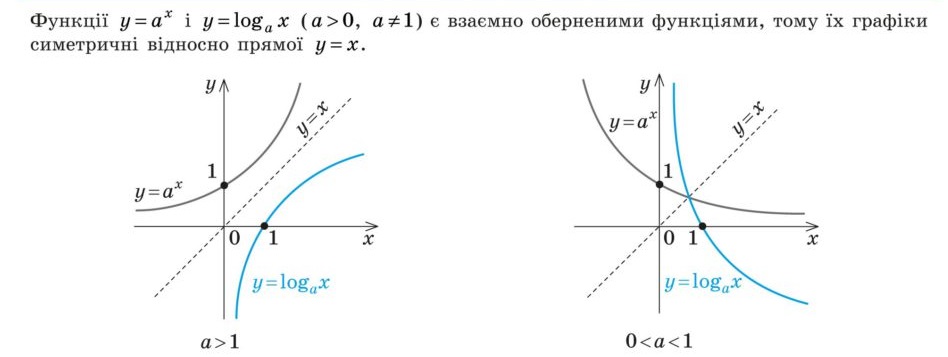
8 Обернена функція Для функції \( y = a^x \) оберненою є логарифмічна функція \( x = \log_a y \).

Властивості логарифмічної функції

№ВластивістьОпис
1Область визначенняФункція \( y = \log_a{x} \) визначена для \( x > 0 \), тобто \( D(y) = (0; +\infty) \).
2Область значеньЗначення функції може бути будь-яким дійсним числом, тому \( E(y) = \mathbb{R} \).
3Зростання або спадання
  • Якщо \( a > 1 \), то функція \( y = \log_a{x} \) є зростаючою.
  • Якщо \( 0 < a < 1 \), то функція \( y = \log_a{x} \) є спадною.
4Поведінка при \( x \to 0^+ \) та \( x \to +\infty \)
  • При \( x \to 0^+ \), функція прямує до \( -\infty \).
  • При \( x \to +\infty \), функція прямує до \( +\infty \).
5Перетин з віссю ординатФункція не перетинає вісь ординат, оскільки вона не визначена для \( x = 0 \).
6Неперервність і диференційованістьФункція є неперервною і диференційованою на області визначення \( (0; +\infty) \).
7АсимптотаГоризонтальна асимптота відсутня, але є вертикальна асимптота при \( x = 0 \).
8Обернена функціяОберненою функцією до \( y = \log_a{x} \) є показникова функція \( y = a^x \).